Travelling salesman problem
Created: 2008-06-19 - 16:56
Travelling salesman problem
(resp. jeho lightova verzia)
Zadanie: Obchodny cestujuci putuje z mesta do mesta. Jeho cielom je vytvorit si taku obchodnu trasu, aby navstivil kazde mesto prave raz a vratil sa do povodneho, z ktoreho vychadzal. Tato light verzia predpoklada, ze vzdialenosti medzi mestami su 1, cize uplne odpada vyber najkratsej moznej trasy (t.z. moze existovat viacero rieseni / rovnako ako ziadne).
Riesenie: Klasicky brutebacktrack so zlozitostou O(n!) postupne vytvara zoznam vrcholov, ktorymi treba prejst.
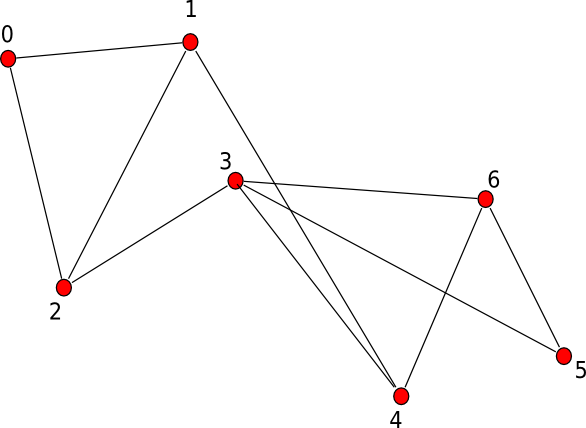
Vychadzal som z tohto grafu:
import java.util.*; public class Pisomka { static int[][] cesty = new int[7][7]; static boolean[] navstivene = new boolean[7]; static int start; static ArrayList<Integer> konecnaCesta = new ArrayList<Integer>(); static Set<ArrayList<Integer>> vysledok = new HashSet<ArrayList<Integer>>(); public static void main(String[] args) { //na zaciatku vynulujeme hodnoty hran a navstivenych vrcholov for(int i=0;i<7;i++){ navstivene[i]=false; for(int j=0;j<7;j++) cesty[i][j]=0; } //rucne zadavame hrany do matice susednosti (kedze ide o neorientovany graf //tak treba aj opacnu hranu zadat...) cesty[0][1]=1; cesty[1][0]=1; cesty[0][2]=1; cesty[2][0]=1; cesty[1][2]=1; cesty[2][1]=1; cesty[1][4]=1; cesty[4][1]=1; cesty[2][3]=1; cesty[3][2]=1; cesty[3][4]=1; cesty[4][3]=1; cesty[3][5]=1; cesty[5][3]=1; cesty[3][6]=1; cesty[6][3]=1; cesty[6][4]=1; cesty[4][6]=1; cesty[5][6]=1; cesty[6][5]=1; //oznacime si od ktoreho vrcholu chceme hladat start = 1; //samotna metoda hladajCestu(start); } public static void hladajCestu(int vrchol){ //zaciname inicializaciou vyberu dalsieho vrchola //kedze ich mame 6 tak pouzijeme for cyklus aby sme nasli ten spravny for(int i=0;i<7;i++){ //nebudeme testovat vrchol sameho zo sebou if(i!=vrchol){ //ak nie je zoznam vrcholov aktualnej cesty naplneny if(konecnaCesta.size()<7){ //ak splna vrchol i podmienku ze je spojeny s vrcholom "vrchol" //a este nebol navstiveny if(cesty[vrchol][i]!=0 && navstivene[i]==false){ //pridaj ho do zoznamu aktualnej cesty konecnaCesta.add(i); //oznac ho za navstiveny navstivene[i]=true; //skus dalsi vrchol hladajCestu(i); //toto sa vykona az ked sa ukonci vetvenie rekurzie //to znamena vtedy ak sa neda pohnut z vrchola na iny vrchol //cize nastavime dany vrchol (kedze velkost listu je 7 tak -1) navstivene[konecnaCesta.get(konecnaCesta.size()-1)]=false; //a odoberieme ho zo zoznamu konecnaCesta.remove(konecnaCesta.get(konecnaCesta.size()-1)); } } //toto sa vykona ked je ArrayList plny else{ //ked je posledny vrchol ten z ktoreho sme zacali if(konecnaCesta.get(konecnaCesta.size()-1)==start){ //pridame danu cestu do mnoziny vsetkych moznych ciest if(!vysledok.contains(konecnaCesta)){ //pridaj ju do vyslednej mnoziny vysledok.add(konecnaCesta); //a vypis ju System.out.println(konecnaCesta); } } } } } } }